What is Break-Even Point, and Why Does It Matter?

The Break-Even Point is an essential financial figure that reflects the level at which a business can operate without making a profit or incurring a loss. In layman’s finance, it refers to a point where income equals cost. BEP is used in business planning and financial management to explain potential successful activity minimum standards in business planning and financial management.

A business needs to understand BEP to understand its cost model and revenue generation. Hence, whether you are thinking about founding a new venture or are currently operating one, break-even analysis should never be left off the list of strategic tools for achieving better financial results.

What is the Break-Even Point?

The break-even point is the sales level that describes the situation when the total costs of production coincide with total revenue. BEP stands for break-even point, and it is an essential aspect of cost accounting that must be considered to get a clear view of a business’s performance.

Although break-even analysis does not provide the exact amount of sales needed to cover all costs, it is important because it helps make decisions. Companies use it to determine the achievable sales volume accurately, choose the right pricing model, and assess their financial liabilities. Consequently, break-even point analysis makes it easy for the company to determine excessive costs, estimate profitability, and even make the right investment decisions.

Formula for Break-Even Point

BEP (Units) = Fixed cost/ (Selling price per unit – variable cost per unit)

Where:

• Fixed Costs: Are those that do not change with the level of production or sales volume, such as rent or salaries.
• Selling Price per Unit: The rate at which the company charges its customers for each unit of product they purchase.
• Variable Costs: Expenses that rise and fall with production volume, such as material or direct people costs.

It assists businesses in determining the number of units that must be produced for sale to break even and start making a profit.

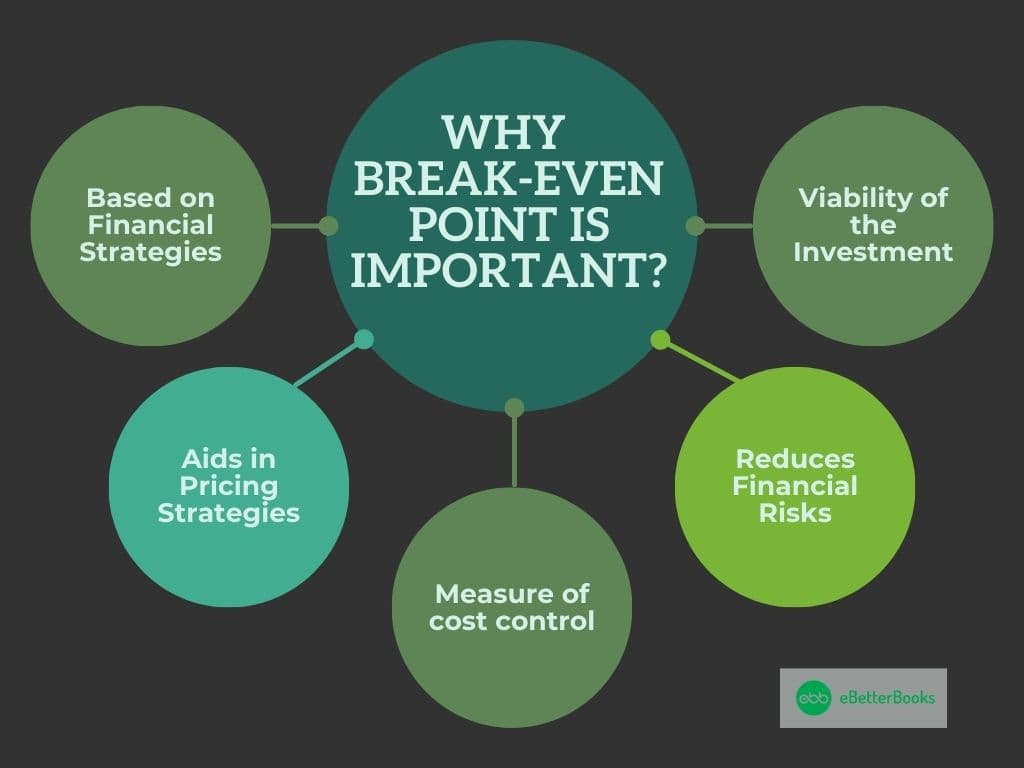
Why Break-Even Point is Important?

Break-even analysis is important to the business because:

• Based on Financial Strategies: The concept of the break-even point is at the base of most financial strategies. It assists practitioners in setting understandable commercial objectives and financial planning due to the definition of the required minimum of sales.
• Aids in Pricing Strategies: BEP Analysis greatly helps in pricing a product or service. Cost structures and contribution margins help businesses set proper prices to charge customers that guarantee profitability without overcharging.
• Measure of Cost Control: Break-even analysis demonstrates fixed and variable costs and their effects on the break-even point. It helps identify problem areas regarding cost controls from top to bottom and thus optimizes them.
• Reduces Financial Risks: The break-even point gives firms an insight into the consequences of a sales reduction or an increase in cost. It is a hedge that wherever information is being used to make certain decisions, it must be accurate information.
• Assesses the Viability of an Investment: Break-even analysis provides a means of determining the probable sales volume necessary for reimbursing costs by assessing the capability of a new product or new market before it is developed.

How Break-Even Analysis Works?

Break-even analysis involves the identification of certain steps to use in determining the amount of sales necessary to attain the total cost.

Here’s how it works:

Distinguish Between Fixed and Variable Costs

Fixed Costs are the same regardless of production or sale and include rent, salaries, and insurance. For example, if a business’s rent is $5000 a month, it will remain the same whether the company sells just one item or thousands.

Variable Costs vary with output levels. Other examples include raw materials, packaging expenses, and labor costs directly associated with production. If the variable cost per unit is $10, it rises with the number of units produced.

Apply the Formula

The break-even point is calculated using this formula:

Break-Even Point (Units) ≡ Fixed Costs / (Selling price – Variable price).

For example, if a company has fixed costs of $20,000, sells a product for $50, and incurs a variable cost of $30 per unit:

BEP = $20,000 / ($50 – $30) = 1,000 units

Interpreting the Results

Knowledge of BEP thus enables managers to set sales goals for products to be sold, incentivize employees, and ascertain their affordability.

For instance:

So if the company sells over 1000 units, it is in the black.

The company sells less than 1000 units, which is a loss.

It informs price-setting decisions, cost control, and, generally, business planning.

Example of Break-Even Analysis

Let there be a small bakery that has fixed costs of $ 10,000 (rent, salaries, etc.) and a marginal cost of $2 per cupcake.

If the bakery sells each cupcake for $5, its break-even point is:

BEP = Fixed Costs / (Selling Price – Variable Cost)

BEP= $10000/ ($5.00-$2.00) = 3334 cupcakes

This tells us that the bakery has to sell 3,334 cupcakes on average every month if they’re to turn a profit. Anything in excess of this amount is profitable, while the sale below this results in a loss.

For instance, if the bakery sells 4,000 cupcakes, its profit is:

Profit= (4000 x $ 3) + (- $ 10,000) = ($2,000)

This example shows the usefulness of break-even analysis by offering information for production, pricing, and sales strategies.

Advantages of Break-Even Analysis

Break-even analysis is very beneficial for a business, and the following points can understand it:

• Simplifies Financial Goals: For financial and managerial reasons, it offers definite goals for the company’s sales and income levels that can guarantee its profitability.
• Identifies the Impact of Cost Changes: This will help businesses appreciate that a shift in costs or prices can affect the break-even point.
• Enhances Strategic Decision-Making: Depending on the business’s BEP outcome, the company can decide whether to alter its pricing strategy, expand, or cut costs.
• Improves Resource Allocation: It helps direct resources only to areas that can improve the organization’s revenue generation.
• Facilitates Risk Management: Compared to other techniques, Break-Even analysis minimizes risks because it presents strategic decision-making with empirical evidence.

How is the Break-Even Point Used?

The break-even point is useful in a lot of discussions in which a business is engaged, like:

• Pricing Decisions: An important use of break-even charts is pricing products and services at competitive rates that will cover the company’s costs and allow it to make reasonable profits. In other words, BEP enables companies to consider cost factors and avoid offering products at too low prices.
• Cost Reduction: BEP stands for Business Efficiency Perspective, which draws attention to inefficiencies in cost structures. For instance, if a business analyzes its variable costs, it may need to seek ways to consolidate its costs, such as bulk buying from suppliers.
• Profitability Forecasting: A result of break-even analysis is a clear picture of the profit potential. New product or service development can help organizations determine whether a specific product or service will generate enough sales to be profitable and is thus a valuable strategic planning tool.

Types of Break-Even Points

There are three break-even calculations:

• Unit-Based Break-Even Point: Mid-tailored attracts interest in the quantity of units required to cover costs. It is obtained by using the standard BEP formula, which is Bandwidth x Elasticity.
• Sales Revenue Break-Even Point: It determines the total revenue required to break even: BEP (Sales Revenue) = Fixed Costs / Contribution Margin Ratio. For instance, where the fixed costs are $30000, and the contribution margin ratio is 40%, the BEP is $75000.
• Multi-Product Break-Even Point: Where the organization offers many products for sale, the BEP is calculated using the weighted averages of the contribution margins. For instance, a firm in the laptop and the bag business determines a total BEP that relies on businesses’ proportions and margins.

Break-Even Point and Contribution Margin

The contribution margin is the difference between the selling price and variable cost per unit:

Contribution Margin = Selling Price, Less Variable Cost Per Unit

For instance, if a product is being sold at $100 and the variable cost stands at $60, then the contribution margin is $40.

Impact on Break-Even Point

An increase in the contribution margin decreases the BEP. Using the formula:

BEP = Fixed Costs / Contribution Margin

If fixed costs are $20,000 and $40 is replaced by $50 as contribution margin, the BEP decreases from 500 to 400 units.

Example

An organization requires contribution margins of $100 for a designer handbag, which has acquired $20,000 of fixed costs through selling a minimum of 200 units. If the target margin is increased to $120, the BEP will only be 167 units.

What Causes a Company’s Break-Even Point to Increase?

There are many reasons which can cause the break-even point to rise, which are:

• High Fixed Costs: Costs such as rent, wages, or equipment leases increase the BEP. For example, expanding to a bigger office or employing more people increases the revenue needed for expenditures. 
• Increased Variable Costs: These include costs of raw materials, production, and human resource costs that, when changed, affect BEP. For instance, if material prices per unit go up from $20 to $25, the BEP is also likely to change.
• Lower Selling Price: Seasonal sales, sales promotions, and discounting impact the contribution margin, which is the selling price—variable cost per unit—and increase the BEP. For instance, when a product is selling at $50 per unit, a drop to $45 means that even the business must sell more units.

How to Reduce Break-Even Point?

There are a few ways to reduce breakeven, which are:

• Lower Fixed Costs: Opt for flexible working, negotiate rent, or outsource activities that are not part of the core business output to minimize overhead expenses. For example, operating from a business incubation hub means paying less rent.
• Decrease Variable Costs: Methods for controlling variable costs include buying supplies in large quantities, offering suppliers new terms of business, or automating the manufacturing process. For instance, acquiring supplies at a lower price per unit can lower total expenses per unit.
• Increase Selling Price: However, frequent price increases can offset any benefits provided by BEP, so the changes in price must be justified by the perceived value added to products or services by the customer.

Conclusion

Being a perfect tool for making strategic decisions and gaining the necessary clarity in businesses’ financial plans, the break-even point deserves attention. That’s why, knowing and using BEP analysis, it is possible to establish real sales targets, work with costs, and predict many dangers. Be it pricing policies, cut-throat cost reductions, or predicting profitability, break-even analysis guarantees the derivative of the right decisions and, hence, route to growth.

FAQs

Why is a Lower Break-Even Point Better?

A low BEP shows that a business requires fewer units or even lower revenue to reach a particular break-even point, minimizing the financial risks involved and making profits more achievable.

What Happens if There is No Break-Even Point?

If a business cannot come up with a break-even point, then it means that as much as revenue is generated, total costs are always higher than revenue. Hence, we are dealing with a business that is perpetually in the red. This shows that business operations are rather unsustainable, and these strategies require some changes.

Is a High Break-Even Point Good?

High sales volumes are also undesirable because they increase the sales volume needed to achieve the break-even point. This could be a concern, especially when the organization is in a business that experiences volatility in demand.

What is the Normal Profit at the Break-Even Point?

At the break-even point, the firm’s profit is zero. This is because operating revenue equals operating expenses, and neither covers other costs except for exigent circumstances.